wiwaxia

Il y a parfois des sujets qui surgissent d'une manière sporadique sur les forums, comme cela vient encore de se produire il y a quelques jours: la question de savoir si un point se trouve dans un triangle, initialement exprimée en juin 2003 (cinq messages), a suscité une correction de code en juillet 2009, puis deux questions en mai 2011 (malheureusement restées sans réponse) et tout dernièrement la mention d'un lien sur la Toile.

Je venais moi-même de poster un commentaire lorsque m'est apparu l'étalement des dates (14 ans ! ) ... D'où un retrait immédiat du message, conscient du ridicule achevé de la situation, et de ce que la généralisation d'une telle pratique dénaturerait complètement les échanges sur les forums.

Rien à voir évidemment avec l'intérêt de la question, parfois exprimée en d'autres occasions. et à laquelle d'autres intervenants ont apporté de bonnes réponses. Ce sont quelques développements particuliers qui me sont venus en tête.

# Dans le plan (xOy) d'un repère orthonormé direct (Oxyz) contenant le triangle (ABC) et un point quelconque (M), la recherche de la réponse passe évidemment par le calcul de trois déterminants (ou produits mixtes, ce qui revient au même):

Q_A = Det(MB, MC) = u_z│(MB×MC) ,
Q_B = Det(MC, MA) = u_z│(MC×MA) ,
Q_C = Det(MA, MB) = u_z│(MA×MB) .

(M) appartenant à (ABC) si et seulement si les trois termes précédents possèdent le même signe, et vérifient par conséquent la condition:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

Test:= ((Qa*Qb>0) AND (Qb*Qc>0))

Les triangles (MAB), (MBC) et (MCA) présentent alors la même orientation intrinsèque, identique à celle de (ABC); ils sont tous directs quand les déterminants sont positifs, rétrogrades dans le cas contraire.

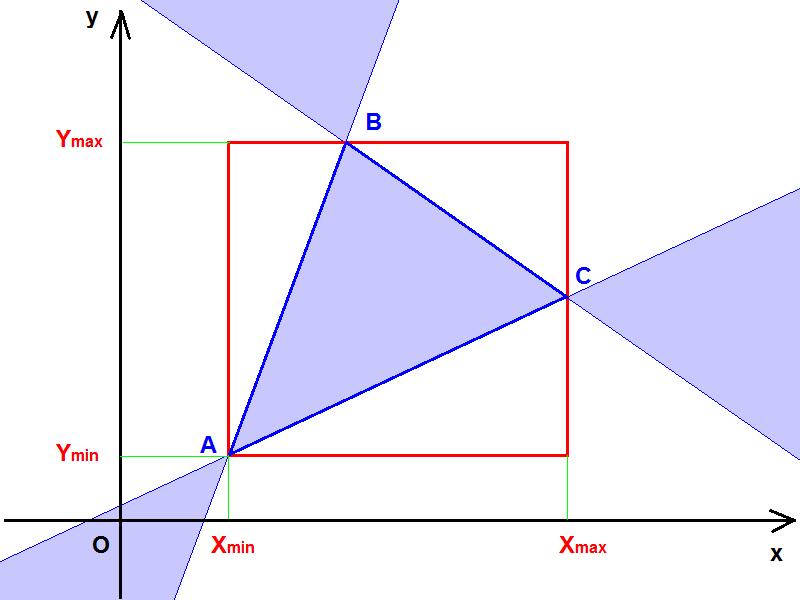
# Toutefois lorsqu'un grand nombre de vérifications s'avère nécessaire, un autre test permet de se dispenser souvent du calcul précédent par le rejet préalable des points (M) situés à l'extérieur du rectangle circonscrit au triangle (ABC), et d'arêtes parallèles aux axes (x'x, y'y).
Il suffit de déterminer les valeurs extrêmes des coordonnées des 3 sommets:
X_min = Min(X_A, X_B, X_C) , X_max = Max(X_A, X_B, X_C) , etc ...
puis d'effectuer le test:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

Test1:= ((Xmin<x) AND (x<Xmax)) AND ((Ymin<y) AND (y<Ymax))

La condition d'intériorité au triangle (ABC) intervient ensuite - et seulement dans ce cas:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

Test2:= ((Qa*Qb>0) AND (Qb*Qc>0))

(le second test est vrai dans les zones bleutées du graphe).