par , 08/05/2017 à 20h01 (1241 Affichages)
Suite du billet précédent.
# Une autre variante, beaucoup plus efficace, consiste à diminuer les valeurs concernées (au lieu de les augmenter), sur un choix aléatoire indépendant de la position, de la forme et de l'étendue du triangle; le critère portera par exemple sur la somme des coordonnées des sommets (modulo M), en faisant par exemple intervenir la fonction booléenne :
1
2
3
4
5
6
7
8
|
FUNCTION PlusTabc(Lim: Byte; V1, V2, V3: Point): Boolean;
VAR t: Byte; Somme: LongInt;
BEGIN
Somme:= V1.x + V1.y; Inc(Somme, (V2.x + V2.y));
Inc(Somme, (V3.x + V3.y)); t:= Somme MOD 128;
PlusTabc:= (t<Lim) // Lim = 0: aucun positif
END; // Lim = 128: tous |
puis en codant dans le balayage du rectangle circonscrit:
1
2
3
4
5
| ...
Test2:= PlusTabc(Seuil, VeA, VeB, VeC);
IF Test1 THEN BEGIN
IF Test2 THEN Inc(C_[VeM.x, VeM.y])
ELSE Dec(C_[VeM.x, VeM.y]); ... |
Pour une valeur de Seuil égale à 96, il se produit statistiquement 96 incrémentations (soit en moyenne dans 96/128 = 75 % des cas) et 32 décrémentations (événement trois fois moins probable: 25 %).
Voici deux séries d'images obtenues pour les domaines [0 ; Zmax] et [Zmax/2 ; Zmax], pour des nombres de tirages respectivement égaux à:
N1 = 128 , N2 = 1024 , N3 = 8192 et N4 = 65536:
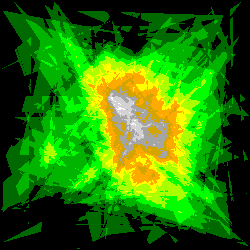
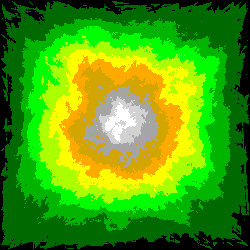
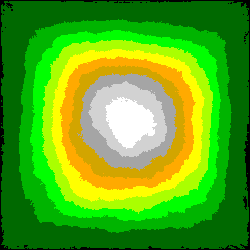
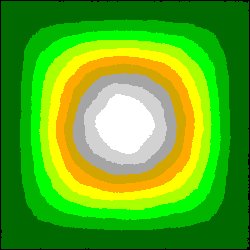
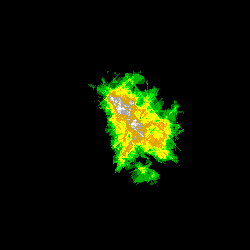
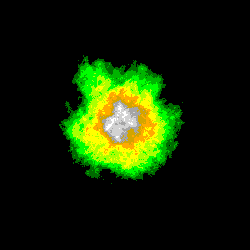
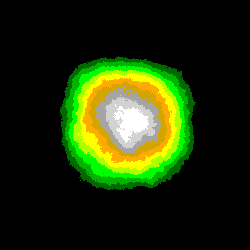
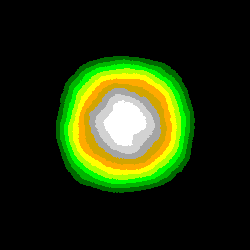
Noter l'apparentement des contours observables dans la partie centrale des images de même rang.
On peut comparer ces images, parce que le calcul de chacune d'entre elles a été précédé de la ré-initialisation du générateur de nombres pseudo-aléatoires à la même valeur de la graine:
La dernière série montre l'évolution de l'image précédente (N = 65536, intervalle [Zmax/2 ; Zmax]) pour des valeurs de Seuil de plus en plus faibles:
S1 = 80 , S2 = 72 , S3 = 68 , S4 = 67 ,
la probabilité d'incrémentation diminuant de (80/128 = 62.5 %) à (67/128 = 52.3 %):
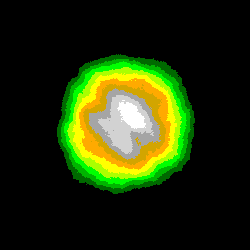
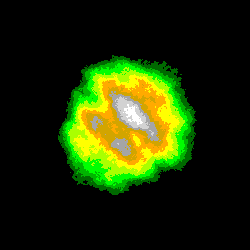
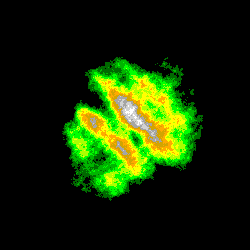
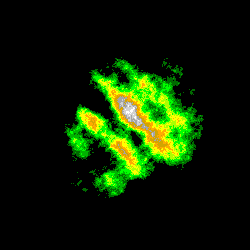
Une plus longue série d'images (c'était prévu, mais la place manquait) eût encore mieux montré le morcellement progressif des contours lorsque le seuil diminue et se rapproche de la valeur critique (64); la fragmentation observée est liée à l'importance croissante des fluctuations d'un système stochastique autour de sa valeur moyenne: on obtient en effet à la limite (SLim = M/2 = 64): Zmoyen = 0 .











