User

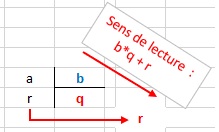
À deux entiers naturels a et b, on associe de façon unique deux entiers naturels : le quotient q et le reste r, qui vérifient :
a = bq + r ;
r < b.

En VBA on obtient le quotient q en appliquant l'opérateur de division entière \ entre a et b : q = a \ b.
Le reste s'obtient en appliquant l'opérateur mod entre les 2 entiers : r = a mod b .




I - Conversion en heures et minutes d'une durée exprimée en minutes

On souhaite exprimer cette durée d en h heures et m minutes de façon à avoir : d = 60*h + m

1 heure étant égale à 60 minutes

On remarque que nous avons une expression de la forme a = bq + r, avec a=d et b=60.
Cela revient donc à réaliser une division euclidienne de d par 60, avec le quotient q=h et le reste r=m.

Prenons d=150, on a d'après la formule du quotient : q = h = 150 \ 60 = 2.

et d'après la formule du reste : r = m = 150 mod 60 = 30.

En substituant les valeurs dans d = 60*h + m, on obtient bien : d = 60*2 + 30 = 150.



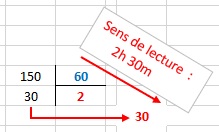
Conclusion :

d est égal à 2 heures et 30 minutes


II - Conversion en heures, minutes et secondes d'une durée exprimée en secondes

On souhaite exprimer cette durée en h heures, m minutes et s secondes de façon à obtenir : d = 3600*h + 60*m + s.

on peut dans un premier temps traduire cette expression sous une forme euclidienne comme ceci :

d = 3600*q1 + (60*q2 + r2) équivaut à d = 3600*q1 + r1 avec r1 = (60*q2 + r2).

où q1 représente le quotient de la division euclidienne de d par 3600 et r1 = m*60 + s représente le reste de cette division.

Prenons d = 4000 secondes

on a d'après la formule du quotient : q1= 4000 \ 3600 = 1, donc h=q1=1

et d'après la formule du reste : r1= 4000 mod 3600 = 400

d'où : r1 = 60*m + s = 400

On va donc à nouveau réaliser une division euclidienne de 400 par 60 :

on obtient m = 400 \ 60 = 6 et s = 400 mod 60 = 40

finalement :

d=3600*1 + 60*6 + 40 = 4000

Selon le schéma :



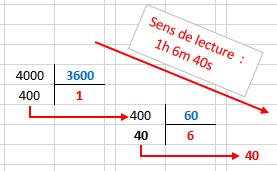
Conclusion :

d est égal à 1 heure 6 minutes et 40 secondes


III - Conversion d'un nombre décimal en binaire

Plus généralement, un nombre décimal par exemple 14 peut s'écrire sous la forme de puissance de 2 :

14 = (2^3)*1 + (2^2)*1 + (2^1)*1 + (2^0)*0 avec 2^3=2*2*2=8.

soit en binaire 1110.

cette expression est de la forme :

a = b1*q1 + b2*q2 + b3*q3 + b4*q4 + r4 avec r4=0.

dans laquelle les valeurs q1, q2, q3, q4 s'obtiennent en appliquant des divisions successives selon le schéma :



On voit qu'on peut identifier une relation de récurrence :

a1 = b1*q1 + r1

----ordre 2 -> r1 = a2 = b2*q2 + r2

-------------------------------ordre 3 -> r2 = a3 = b3*q3 + r3
...

Plus généralement, en introduisant les notations :

q(i) et r(i) pour quotient et reste d'ordre i, avec i prenant successivement les valeurs de 1, 2, 3...

On peut alors écrire :

a(i) = b(i)*q(i) + r(i)

--------------------r(i) = a(i+1) = b(i+1)*q(i+1) + r(i+1)

-----------------------------------------------------------r(i+1) = a(i+2) = b(i+2)*q(i+2) + r(i+2)

cette expression générale de la forme :

a = b(1)*q(1) + b(2)*q(2) + b(3)*q(3) + ...+ b(n+1)*q(n+1) + r(n+1), où n est l'exposant de poids fort du nombre binaire, donné par log(a)/log(2).

avec b(1)=2^n, b(2)=2^(n-1),...,b(n+1)=2^(0), et b(n+1)*q(n+1)=q(n+1).

nous permet d'écrire la fonction générale de conversion d'un nombre décimal en binaire :

Code VBA :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Public Function convDecEnBin(ByVal a As Long, _
              Optional nbPositions As Variant) As String
    ' Fonction de conversion d'un nombre décimal en binaire, on peut indiquer le nombre de positions binaires que l'on souhaite obtenir
    Dim n As Long ' exposant de 2 du bit de poids fort, nombre de positions -1
    Dim q As Long, r As Long ' Quotient et reste de la division euclidienne
    Dim b As Long ' entier b diviseur de 2^n à 2^0=1.
    ' 10 = 1*2^3 + 0*2^2 + 1*2^1 + 0*2^0
    n = Int(Log(a) / Log(2)) ' on détermine l'exposant de 2 du bit de poids fort (tel que : a = 2^n)
    r = a
    b = 2 ^ n ' 1er diviseur
 
    convDecEnBin = vbNullString ' on initialise la chaine destinée au futur nombre binaire
    While b <> 0 ' on parcourt les positions du bit de poids fort 2^n au bit de poids le plus faible 2^0=1
        q = r \ b ' calcul du quotient de la division
        r = r Mod b ' calcul du reste de la division
        convDecEnBin = convDecEnBin & q ' on ajoute le bit en bout de chaîne
        b = b \ 2 ' diviseur : 2^i
    Wend
 
    If Not IsMissing(nbPositions) Then ' si on a demandé un nombre précis de positions binaires
        If n + 1 > nbPositions Then ' si le nombre de positions attendu est inférieur au nombre réel
            ' affiche un message d'erreur
            convDecEnBin = "Erreur - Le nombre excède le nombre de bits attendu"
        Else
            ' formate le nombre binaire en fonction du nombre de bits attendu
            convDecEnBin = Right$(String$(nbPositions, "0") & convDecEnBin, nbPositions)
        End If
    End If
 
End Function

Optimisation suivant un schéma de Hörner :

On peut aussi utiliser une méthode plus performante mais un peu moins facile à présenter.
Si on reprend l'exemple précédent de conversion du nombre 14 en binaire, le schéma des divisions successives devient :



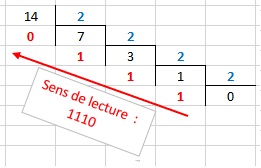
On lit les restes des divisions successives dans le sens contraire de leur obtention pour constituer le nombre binaire.

Le polynôme s'écrit alors :

a = ((r4*2 + r3)*2 + r2)*2 + r1 qui est de la forme a = q1*2 + r1 avec q1 = ((r4*2 + r3)*2 + r2) etc..

On voit qu'on peut identifier successivement q1, q2, q3,... :

ordre 1 -> a1 = q1*2 + r1

ordre 2 -> q1 = q2*2 + r2

ordre 3 -> q2 = q3*2 + r3
...

L'expression générale est donc de la forme : a = (((...(r(n+1)*2 + r(n))*2...)*2 + r(3))*2 + r(2))*2 + r(1).

On remarque que suivant cette méthode les restes sont obtenus dans l'ordre inverse de la 1re méthode.

Cette formule nous permet d'écrire en VBA la fonction de conversion suivant ce schéma :

Code vba :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
Public Function convDecEnBinHorner(ByVal a As Long, _
              Optional nbPositions As Variant) As String
    ' Fonction de conversion d'un nombre décimal en binaire suivant Hörner, on peut indiquer le nombre de positions binaires que l'on souhaite obtenir
    ' Inspiré du code de Randy Birch (MVP Visual Basic)
    Dim n As Long ' exposant de 2 du bit de poids fort
    Dim q As Long, r As Long ' Quotient et reste de la division euclidienne
    Dim b As Long ' entier b diviseur
    b = 2
    q = a
 
    convDecEnBinHorner = vbNullString ' on initialise la chaine destinée au futur nombre binaire
    While q <> 0 ' on parcourt les positions du bit de poids fort au bit de poids le plus faible
        r = q Mod b ' calcul du reste de la division
        q = q \ b ' calcul du quotient de la division
        convDecEnBinHorner = r & convDecEnBinHorner   ' on ajoute le bit en bout de chaîne
    Wend
 
    If Not IsMissing(nbPositions) Then ' si on a demandé un nombre précis de positions binaires
        If Len(convDecEnBinHorner) > nbPositions Then ' si le nombre de positions attendu est inférieur au nombre réel
            ' affiche un message d'erreur
            convDecEnBinHorner = "Erreur - Le nombre excède le nombre de bits attendu"
        Else
            ' formate le nombre binaire en fonction du nombre de bits attendu
            convDecEnBinHorner = Right$(String$(nbPositions, "0") & convDecEnBinHorner, nbPositions)
        End If
    End If
 
End Function