Discussion :

[dridri85]

Bonsoir,
j'ai un problème bien particulier pour obtenir des coordonnées cartésiennes à partir de 2 angles.
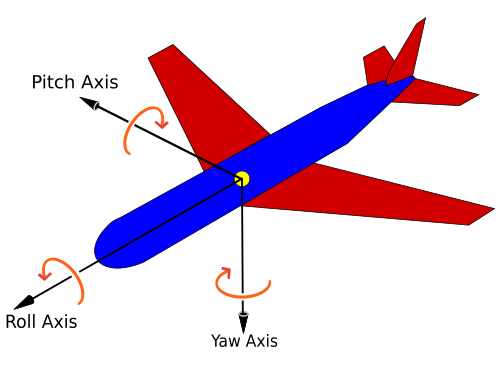
C'est pour les utiliser dans un jeu en 3D: le principe du jeu est simple, il faut piloter un avion dans un univers (là n'est pas la question), pour contrôler mon avion j'ai la possibilité de modifier le roulis et le tangage de l'appareil ce qui me donne deux angles.
(le roulis c'est l'inclinaison gauche/droite, le tangage l'inclinaison vers le haut/bas).
J'ai besoin de récupérer les coordonnées du nez de l'avion (supposons qu'il se trouve à 1 unité du centre de gravité) à partir des deux angles, ce qui me permettra d'obtenir le vecteur de l'avion. Le problème est qu'il faut d'abord prendre en compte le roulis puis le tangage (pour tourner l'avion se penche sur le coté, puis "monte").
Et je n'ai rien trouvé de satisfaisant...

Merci

[Alp]

Tu ne serais pas en train d'utiliser des coordonnées sphériques (polaires c'est en 2D) par hasard ?

Si tu as la distance entre l'origine et le nez, tu peux obtenir très facilement la position du nez de l'avion en coordonnées cartésiennes.

[dridri85]

Exact ce sont des coordonnées sphériques (je change le titre du topic de suit, merci)

Et oui je connais la distance entre l'origine et le nez, donc comment je fais ?

[pseudocode]

Le problème est qu'il faut d'abord prendre en compte le roulis puis le tangage (pour tourner l'avion se penche sur le coté, puis "monte").
Et je n'ai rien trouvé de satisfaisant...

Étonnant que tu ne sois pas tomber sur les "angles d'Euler" dans ta recherche, en particulier la notation Yaw/Pitch/Roll (convention de Tait-Bryan).

[Pistolero_JB]

Une petite animation interactive sur les angles d'Eulers peut aider à visualiser le problème ici. Dans l'animation le roulis correspond à Psi, le tangage à Theta et le nez de l'appareil est symbolisé par Z2.

Ensuite tu regardes dans wikipedia http://fr.wikipedia.org/wiki/Coordonnées_sphériques, dans la section rayon-longitude-latitude (équivalent à rayon, tangage, roulis) il y les équations de conversions en coordonnées cartésiennes.

A+