Salut
je voudrais ressortir le code recursif qui permettrait de calculer le determinant d'une matrice carrée. Par exple:
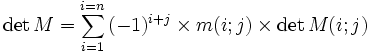


Salut
je voudrais ressortir le code recursif qui permettrait de calculer le determinant d'une matrice carrée. Par exple:
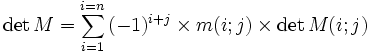
Moi, là, je mangerais plutôt une bonne entrecôte sauce roquefort.
Nous ne sommes pas là pour écrire ton code. Si tu as un problème au niveau algorithmique, il y a un forum dédié. Par contre, si tu as déjà écris une partie du code, tu peux poser des questions spécifiques sur les zones qui posent problèmes...Envoyé par NThierry
Jc
Je le dis tout de suite, je ne sais plus calculer le déterminant d'une matrice, mais, pour te mettre sur la voie, voici le principe de base d'une fonction récursive
Code : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
8
9
A méditer: La solution la plus simple est toujours la moins compliquée
Ce qui se conçoit bien s'énonce clairement, et les mots pour le dire vous viennent aisément. Nicolas Boileau
Compiler Gcc sous windows avec MinGW
Coder efficacement en C++ : dans les bacs le 17 février 2014
mon tout nouveau blog
Je suppose que i représente les lignes et j les colonnes d'une matrice carrée m. Voici une partie d'idée d'algo, je te promets rien:je voudrais ressortir le code recursif qui permettrait de calculer le determinant d'une matrice carrée. Par exple:
Ensuite, faudrait aussi que tu me dises à quoi correspond "detM(i,j)". que doit contenir ce tableau à deux dimensions? La valeur du déterminant ligne i, colonne j, ca me semble bizarre mais bon ne sais plus trop comment ca fonctionne exactement....
Code : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
8
9
10
11
12
13
j ai resolu ton probleme
voila le main.c et main.h correspondants
Code : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
et main.h
Code : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
maintenant avec ces fonctions tu peux resoudre tout systeme de cramer d equations, si tu veux je peux te faire le code aussi pour ça
voici donc le code pour resoudre par la methode de cramer un systeme de n equations lineaire à n inconnues, autant vous dire qu il ne faut pas faire comme ça si n est trop grand sinon ça plante
main.c
Code : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
et le fichier header main.h
Code : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
je suis debutant, qui peut m expliquer pourquoi le programme precedent fait exploser la memoire semble t il des que n=6 (le programme cree plein de matrices intermediaires il est vrai mais quand meme)
merci
Fait une recherche dans le forum "Algorithme".
On a eu le cas de quelqu'un qui cherchait à calculer le déterminant d'une matrice et il est apparu, après discussion avec des membres ayant vraisemblablement un bon niveau en math (en tous cas meilleur que le mien) que la formule que tu veux utiliser est très belle (compacte et récursive) mais que ce n'est pas la méthode la plus efficace niveau temps de calculs pour calculer le déterminant d'une matrice (il y en a une autre, avec des pivots façon Gauss).
Sinon, si tu cherches vraiment à implémenter cette fonction à partir de la formule du premier message (tirée de wikipedia), il est tout à fait possible d'économiser beaucoup de mémoire en utilisant toujours la même matrice (pas de recopie) mais en ne conservant dans les appels de fonction que les listes des lignes/colonnes que l'on souhait garder pour le calcul). Il n'empèche que l'autre méthode se révèle quand même beaucoup plus efficace.
"On en a vu poser les armes avant de se tirer une balle dans le pied..."
-- pydévelop
Derniers articles:
(SQL Server) Introduction à la gestion des droits
(UML) Souplesse et modularité grâce aux Design Patterns
(UML) Le Pattern Etat
Autres articles...
Je n'ai pas compilé le code, mais les idées qui viennent tout de suite en tete sont du genreEnvoyé par informatik
-Une fonction récursive, si elle est appelée à de nombreuses occasion, va rapidement saturer le stack (la pile) du processeur, avec pour résultat le fameux "stack overflow"
-Pour chaque matrice de N ligne et M colones (ici, N et M sont identiques, du fait qu'il s'agit d'une matrice carré) on doit réserver N*M éléments.Envoyé par FIXME
Comme la mémoire n'est pas infinie (et, qu'en plus, certains OS limitent la mémoire pour les applications), et que le type double est un type qui, de lui-même demande pas mal de place en mémoire, si chaque appel récursif de la fonction nécessite l'allocation de (N-1)*(M-1) éléments par rapport aux valeurs de la fonction "appelante", on peut effectivement se dire que la mémoire sera vite saturée...
A méditer: La solution la plus simple est toujours la moins compliquée
Ce qui se conçoit bien s'énonce clairement, et les mots pour le dire vous viennent aisément. Nicolas Boileau
Compiler Gcc sous windows avec MinGW
Coder efficacement en C++ : dans les bacs le 17 février 2014
mon tout nouveau blog
Bin dans ce cas faut voir pour transformer la fonction récursive en fonction récursive terminale, cela évite justement de staturer la pile !Envoyé par koala01
Mon Site
Ma bibliothèque de gestion des chaînes de caractères en C
L'imagination est plus importante que le savoir. A. Einstein
Je ne répond à aucune question technique par MP, merci d'avance !
l algorithme recursif de calcul de determinant par detM=Somme(m(i,j)*(-1)^(i+j)*detMi,j) consomme de façon exponentielle de la memoire avec la taille n et exp(6)=403 !
une bonne methode alternative est celle de la triangulation de la matrice par la methode de gauss par exemple
Oui, c'est ce dont je parlais (faire une recherche dans le forum "Algo", le sujet y est peut-être encore...)Envoyé par informatik
"On en a vu poser les armes avant de se tirer une balle dans le pied..."
-- pydévelop
Derniers articles:
(SQL Server) Introduction à la gestion des droits
(UML) Souplesse et modularité grâce aux Design Patterns
(UML) Le Pattern Etat
Autres articles...
je suis vraiment debutant et j aimerais qu on m explique ce que c est une fonction recursive terminale et comment ça se programme ? merciEnvoyé par Franck.H
C'est un problème d'algorithme, pas de langage. On t'a déjà indiqué le bon forum...Envoyé par informatik
Voici un tout petit cours et exemple: Récursivité terminale mais il est clair que c'est avant tout un problème algorithmique !Envoyé par informatik
Mon Site
Ma bibliothèque de gestion des chaînes de caractères en C
L'imagination est plus importante que le savoir. A. Einstein
Je ne répond à aucune question technique par MP, merci d'avance !
Partager