Bonjour à toutes et à tous,
J'ai un ensemble de n noeuds (n pouvant être grand) répartis sur une lattice homogène en 3 dimensions. Chaque noeud de la lattice est distant de son voisin d'une unité (distance=1).
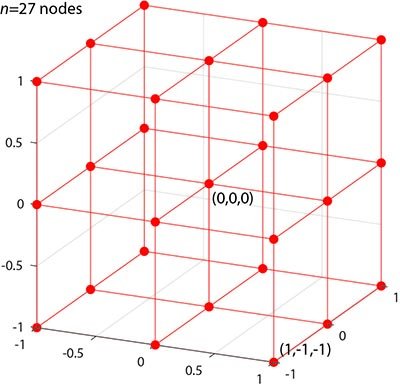
Voici un exemple minimal pour n=27 noeuds
Je cherche à faire correspondre les positions {x,y,z} de chacun de ces points à un index compris dans [0,n]. Cette correspondance doit être bijective et associer chaque tuple {x_i, y_i, z_i} à un index.
Cette question est dans le cadre d'une simulation numérique, et cette opération de correspondance est réalisée un nombre important de fois (de l'ordre de 10^10 au minimum), je cherche donc une correspondance peu couteuse en temps et sans recherche.
Je ne suis pas mathématicien, et en parcourant le net, je vois des topics sur les courbes paramétrées et les hypershères mais je ne comprends pas très bien comment approcher le problème d'un point de vue pratique.
Que me conseillerez vous de faire?
Merci à toutes et à tous d'avance pour vos suggestions.







 Répondre avec citation
Répondre avec citation




















Partager