Discussion :

[gbegreg]

Bonjour,

Il y a quelques années, j'avais publié sur Developpez une série de tutoriels permettant de générer une île en 3D avec Delphi et Firemonkey FMX sland (épisode 1, épisode 2, épisode 3 et épisode 4). Dans ces tutoriels, j'avais utilisé la technique du champ de hauteur (heightmap) et javais complété le projet au fil des épisodes (déplacements, ajouts graphiques, gestion des collisions...).

Aujourd'hui, dans cet exemple, je vous propose une nouvelle fois de générer un terrain en 3D mais cette fois ci de manière procédurale. L'exemple est moins complet que le projet des tutoriels et se concentre uniquement sur la génération du terrain.

Vous trouverez dans le projet exemple, l'unité GBETerrain.pas que j'intègrerai prochainement à ma suite de composants GBE3D pour Delphi.

La génération procédurale de terrain permet potentiellement de générer des terrains de taille illimitée car générés à l'aide de fonctions mathématiques. Pour l'instant, je ne gère pas de niveau de détails (Level of Details en anglais ou LoD).

Passons aux explications.

Tout d'abord, la classe TGBETerrain hérite de TMesh. Notre terrain sera en effet un maillage de type quadrillage de polygones. Nous allons donc devoir calculer les coordonnées X, Y et Z de chaque sommet du maillage.
Les propriétés subdivX et subdivZ indiqueront respectivement le nombre de subdivisions sur l'axe X et sur l'axe Z. Le calcul devra donc déterminer la hauteur Y de chaque sommet.
Les autres propriétés qu'apportent de TGBETerrain au TMesh sont :
- amplitude : permet de fixer l'amplitude maximale que l'on souhaite;
- roughness : permettra de définir la rugosité;
- octaves : nombre d'itération que l'on fera de la fonction getInterpolatedNoise (voir ci après) ;
- seed : permet de donner une racine pour la génération aléatoire;
- XOffset et ZOffset : permettent d’indiquer le décalage sur l'axe X ou Z pour la génération procédurale (par exemple si on souhaite assembler plusieurs TGBETerrain);
- useRamp : la rampe est une image bitmap particulière contenant qu'une seule ligne de 256 pixels. En activant cette propriété à true, alors chaque sommet aura une couleur en fonction de sa hauteur rapportée à cette image de 256 pixels.

Enfin, la classe TGBETerrain fournit également deux procédure : clean (permet de vider le maillage) et generateTerrain (c'est la méthode qui va générer le terrain).

La difficulté principale de ce projet est le rendu naturel d'un terrain à partir de fonctions mathématiques et d'aléatoire. Voici quelques explications.

Tout d'abord, nous avons la fonction noise :

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
 
function TGBETerrain.noise(x, z: integer): single;
begin
  randSeed := x * 9158 + z * 41765 + fSeed;
  result := random * 2.0 - 1.0;
end;

Cette fonction permet de renvoyer un nombre aléatoire entre -1 et 1 en fonction des coordonnées x et z passées en paramètre. Attention, elle pour un couple x,z donné, la fonction doit toujours retourner le même résultat.
Exemple :


Ensuite, la fonction smoothNoise :

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
 
function TGBETerrain.smoothNoise(x, z: integer): single;
begin
  var corners := (noise(x - 1, z - 1) + noise(x + 1, z - 1) + noise(x - 1, z + 1) + noise(x + 1, z + 1)) * 0.125;
  var sides := (noise(x - 1, z) + noise(x + 1, z) + noise(x, z - 1) + noise(x, z + 1)) * 0.25;
  var center := noise(x, z) * 0.5;
  result := corners + sides + center;
end;

Cette fonction permet d'adoucir en regardant le sommet (x, z) et ses 8 voisins (adjacents : haut, bas, gauche, droite et en coin : haut droit, bas droit, bas gauche et haut gauche). On additionne le résultat de noise() de chaque coin puis on lui donne un certain poids.
On fait de même avec les sommet adjacents en donnant un poids plus fort et enfin on donne un poids encore plus fort au sommet que l'on est en train de traiter. Cela permet d'adoucir les différences de hauteurs des sommets voisins.

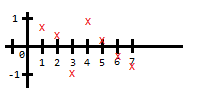
A ce stade, nous avons les hauteurs des sommets. Intéressons nous maintenant à ce qu'il se passe entre ces sommets.
Nous allons interpoler les valeurs entre les sommets. En reprenant le schéma précédent, nous pourrions tracer les droites reliant chaque point. Il s'agit d'une interpolation linéaire et cela ne donnerait pas un résultat très naturel.
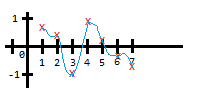
Nous allons utiliser une interpolation cosinus ce qui donnera un résultat comme sur le schéma suivant (courbe bleue).


C'est la méthode interpolate qui s'en charge :

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
 
function TGBETerrain.interpolate(a, b, blend: single): single;
begin
  var theta := blend * PI;
  var f := (1.0 - cos(theta)) * 0.5;
  result := a * (1.0 - f) + b * f;
end;

Cette méthode renvoie la valeur de l'interpolation entre deux valeurs.

Cette fonction est appelée dans la fonction getInterpolateNoise :

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
 
function TGBETerrain.getInterpolatedNoise(x, z: single): single;
begin
  var intX: integer := trunc(x);
  var intZ: integer := trunc(z);
  var fracX := x - intX;
  var fracZ := z - intZ;
 
  { use the near neighbours points v1, v2, v3, v4 }
  var v1 := smoothNoise(intX, intZ);
  var v2 := smoothNoise(intX + 1, intZ);
  var v3 := smoothNoise(intX, intZ + 1);
  var v4 := smoothNoise(intX + 1, intZ + 1);
  { X is the point with x,z coordinates
      v1--------i1---v2
      |         .    |
      |         X    |
      |         .    |
      |         .    |
      |         .    |
      v3--------i2---v4  }
  var i1 := interpolate(v1, v2, fracX);
  var i2 := interpolate(v3, v4, fracX);
  { result interpolate i1 and i2 }
  result := interpolate(i1, i2, fracZ);
end;

Comme schématisé en commentaire dans le code, cette méthode permet d'interpoler en fonction des 4 sommets de la maille traitée.

Enfin, la fonction generateHeight :

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
 
function TGBETerrain.generateHeight(x, z: integer): single;
begin
  var total := 0.0;
  var d := Math.Power(2, fOctaves - 1);
 
  for var i := 0 to fOctaves - 1 do begin
    var freq := Math.Power(2, i) / d;
    var amp := Math.Power(fRoughness, i) * fAmplitude;
    total := total + getInterpolatedNoise(x * freq, z * freq) * amp;
  end;
 
  result := total;
end;

Elle permet d'itérer "octaves" fois sur la méthode getInterpolatedNoise. A chaque itération on prend en compte la rugosité et l'amplitude. Plus il y aura d'itération, plus le terrain sera érodé.

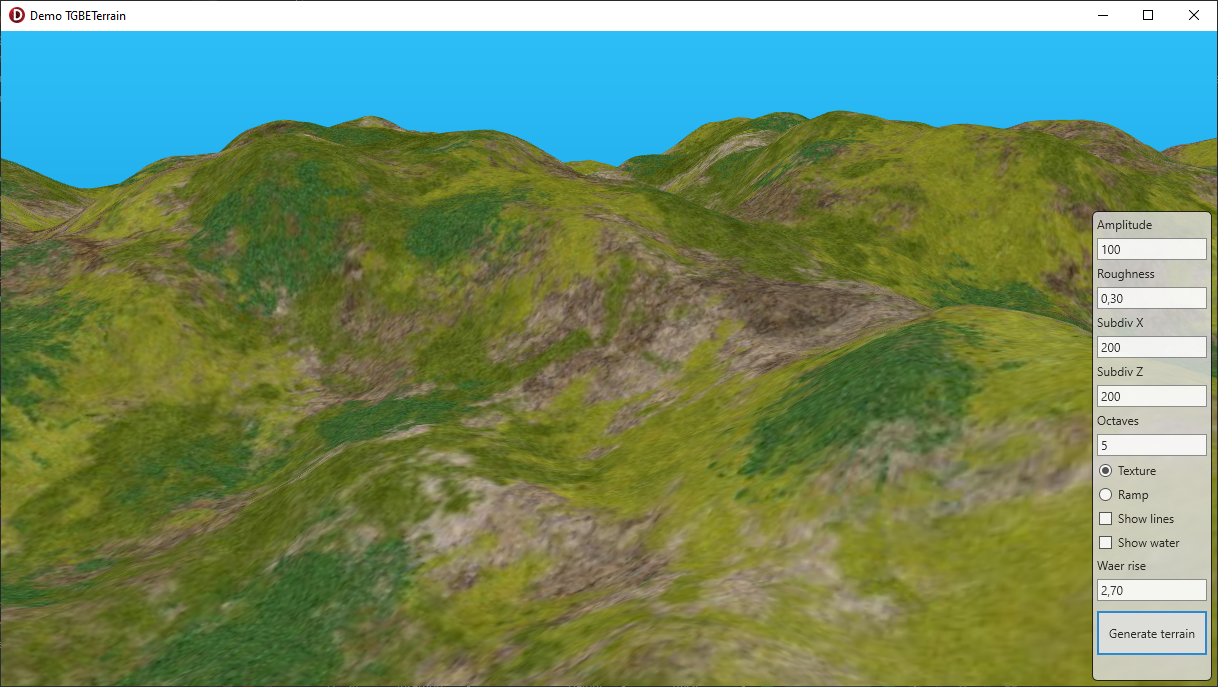
La méthode generateTerrain qui sera en fait la seule à appeler finalement pour générer un terrain crée le maillage et pour chaque maille calcule les coordonnées de chaque sommet via les méthodes vu précédemment.

Voici une capture d'écran de l'exemple fourni :


Le projet est disponible ici en attendant une intégration dans GBE3D : https://www.gbesoft.fr/temp/demoTerrain.zip