Maintenant il s’agit de modéliser les contraintes :
(C1) A la date T, le pilote P conduit seulement la voiture V ;
(C2) A la date T, le pilote P participe seulement à la course C ;
(C3) A la date T, la voiture V est conduite seulement par le pilote P ;
(C4) A la date T, la voiture V participe seulement à la course C ;
Dans le contexte de la théorie relationnelle, ces contraintes s’expriment ainsi :
{P, T} -> {V, C}
{V, T} -> {P, C}
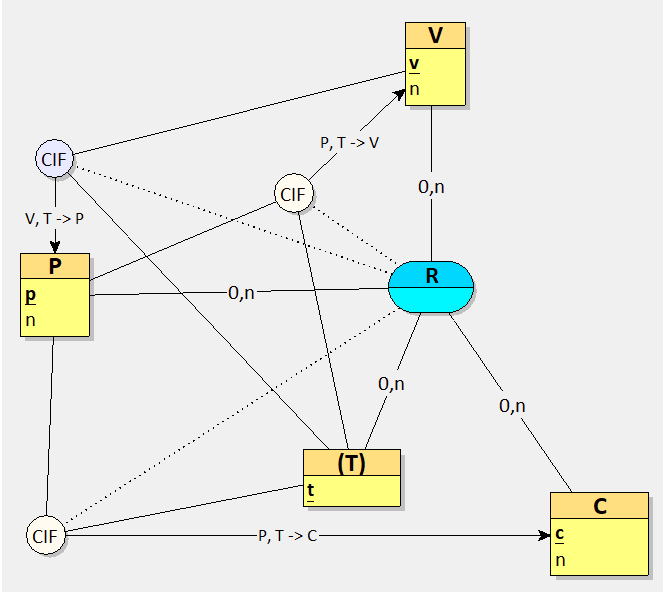
Avec le MCD merisien, l’affaire se corse. Là encore, on utilise des CIF, mais ça devient de la gymnastique.
Il va falloir :
Une 1re CIF pour exprimer la contrainte (C1) : {P, T} -> {V}
Une 2e CIF pour exprimer la contrainte (C2) : {P, T} -> {C}
Une 3e CIF pour exprimer la contrainte (C3) : {V, T} -> {P}
Pas besoin de 4e CIF pour exprimer la contrainte (C4) : {V, T} -> {C}
car Looping manifestement l’infère.
Peut-être peut-on simplifier le MCD dans la mesure où Looping propose des CIF multi-cibles, mais je n’ai pas réussi à mettre en oeuvre cette possibilité. Le MCD ci-dessous peut donner l’envie de partir en courant, mais en tout cas le code SQL produit est correct.
Code SQL (notez la contrainte UNIQUE(v, t) de la table R) traduisant une clé alternative :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| CREATE TABLE P
(
p INT,
n VARCHAR(50) NOT NULL,
PRIMARY KEY(p)
);
CREATE TABLE V
(
v INT,
n VARCHAR(50) NOT NULL,
PRIMARY KEY(v)
);
CREATE TABLE C
(
c INT,
n VARCHAR(50) NOT NULL,
PRIMARY KEY(c)
);
CREATE TABLE R
(
p INT,
t INT,
v INT NOT NULL,
c INT NOT NULL,
PRIMARY KEY(p, t),
UNIQUE(v, t),
FOREIGN KEY(p) REFERENCES P(p),
FOREIGN KEY(v) REFERENCES V(v),
FOREIGN KEY(c) REFERENCES C(c)
); |
Affaire à suivre...
Modèle conceptuel plutôt ambigu [étudiant débutant]
Répondre avec citation
Envoyé par fsmrel
Partager