Discussion :

[Philtheform]

Bonjour, bonsoir,

J'ai une suite de nombres:
47,55,62,79,87,94,...,182,186,199,...,310,314,327,...,458,466,482

Je dois utiliser ces valeurs comme adresse dans un tableau.
La valeur max étant 482, il faut que je crée un tableau avec 482 cellules pour un adressage directe.

Ce que je voudrais, c'est réduire les valeurs proportionnellement à leur grandeur pour limiter le nombre de cellules a créer.

J'ai pensé au logarithme et testé des trucs au pif comme:
tronque[ adr-[(1,6*adr)/Log(adr)] ] avec adr=adresse
ex:47-(1,6*47)/Log(47)=2,026 et tronque(2,026)=2
La liste devient:
2,4,6,12,15,17,...,180,182,186,194 Il y a plus que 194 cellules à créer au lieu de 482

ou autre tentative: tronque[adr-[(3,8*adr)/Ln(adr)]]
0,2,4,10,12,15...172,173,177,185 plus que 185 cellules a créer au lieu de 482

Mon niveau en math n'étant qu’embryonnaire et lointain de surcroît, je me demandais s'il n'existait pas une méthode plus efficace pour réduire au max les valeurs sans avoir de doublons bien évidemment.

Dans la liste il y a 66 valeurs, sans avoir une parfaite égalité, il est peut-être possible de descendre bien en dessous des 185 cellules à créer pour 66 valeurs (119 cellules vides) ?

Désolé si c'est trivial mais je n'arrive pas à formuler mon problème de façon concise pour faire des recherches efficaces sur le net.

En tout cas, merci d'avance pour toute aide.

[wiwaxia]

Bonjour,

... J'ai une suite de nombres:
47,55,62,79,87,94,...,182,186,199,...,310,314,327,...,458,466,482

Je dois utiliser ces valeurs comme adresse dans un tableau.
La valeur max étant 482, il faut que je crée un tableau avec 482 cellules pour un adressage directe. ...

Tu disposes d'une liste ordonnée et finie de (N) nombres entiers. Dès lors que (N) est connu, il te suffit de déclarer une constante tableau de (N) termes, par exemple:

Code Pascal :

Sélectionner tout - Visualiser dans une fenêtre à part

CONST Liste: ARRAY[1..N] OF Word = (47, 55, 62, 79, 87, 94, ..., 182, 186, 199, ..., 310, 314, 327, ..., 458, 466, 482)

ou éventuellement une variable du même type, si tu dois calculer les valeurs entières, ou trier leur liste selon l'ordre croissant.
Cette donnée présentera ainsi le maximum de compacité, et aucune cellule vide.

[Philtheform]

Merci pour la réponse !

Oui, en fait, ma question ne répond pas à mon problème pratique qui est trivial, il y a juste à utiliser la relation d'ordre.

Je suppose que «liste» fait un truc du genre: créer un tableau T[66]={47,55,62,...,482} puis

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
entree=482
for(i=0;i<size_T,i++){
	if(Tab[i]==entree)
		sortie=i
}

Bon, maintenant, le problème mathématique de trouver une fonction qui «comprimerait» une liste de nombres m'intrique toujours. Par «comprimer», j'entends réduire plus fortement les grandes valeurs que les petites et sans que cela ne créer de doublons.

[wiwaxia]

... Bon, maintenant, le problème mathématique de trouver une fonction qui «comprimerait» une liste de nombres m'intrique toujours. Par «comprimer», j'entends réduire plus fortement les grandes valeurs que les petites et sans que cela ne créer de doublons.

Il n'y a pas plus court que la liste précédemment décrite, à moins de travailler en base mixte avec des entiers longs; trois termes consécutifs de la liste initiale seront alors contenus dans l'entier

M_k = N_3k-2*E⁶ + N_3k-1*E³ + N_3k pour k > 0 ;

cela est applicable à tout ensemble de nombres comportant au plus 3 chiffres en notation décimale, et donc majoré par 999.Le plus grand des termes vaut alors:

997998999 < 2147483647 = 2³¹ - 1 .

Le nombre total de termes est alors approximativement divisé par trois: N' = Ceil(N/3) = Trunc(N/3) + 1 .

[Guesset]

Bonjour,

Pourrions nous avoir la liste complète ?

Si la liste ne suit pas une loi particulière (i.e. calculable genre n_i = f(i), la solution qui me vient à l'esprit (esprit es tu là ?) serait une régression (pas nécessairement linéaire). En retirant la valeur trouvée par la fonction issue de la régression, les valeurs absolues de ces différences seront d'autant plus faibles que la fonction sera proche de la loi de distribution des valeurs.

Mais, au sens strict, c'est ce que fait le tableau de wiwaxia. En opérant une recherche dichotomique, il est facile de créer une fonction IndexOf(i: integer) qui retourne -1 si i n'est pas dans le tableau et l'indice dans le tableau en cas de réussite. Il faut au pire 7 comparaisons (66 a le défaut d'être supérieur à 64 = 2⁶).

Salutations

[Flodelarab]

Bonjour

Je n'ai toujours pas compris le vrai but.

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
entree=482
for(i=0;i<size_T,i++){
	if(Tab[i]==entree)
		sortie=i
}

De mon point de vue, cette boucle est inepte. Fais plutôt un tableau associatif. C'est la même idée que wiwaxia, sauf que les clés deviennent les valeurs, et les valeurs deviennent les clés.

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
Tab[47]=0;
Tab[55]=1;
Tab[62]=2;
...
Tab[458]=63;
Tab[466]=64;
Tab[482]=65;
print Tab[entree];

Il n'y a pas de "trous" puisque c'est un tableau associatif.

[Philtheform]

La «liste» est la meilleur solution, oui. La question de la «réduction» c'est juste par curiosité. Je chercherais par moi même quand j'aurais plus de temps tout en risquant de réinventer la roue mais ce n'est pas grave.

Je ne comprends pas le tableau «associatif». Comment l'adresse peut-être 482 dans un tableau qui n'a que 66 cases?

C'était juste pour faire un décompte de façon «directe/fainéante». Je parcours ma liste à analyser et à chaque valeur je fais +1 ds la cellule correspondant à la valeur dans le tableau de décompte. La valeur devient une adresse dans le tableau de décompte et du coup je ne parcours la liste à analyser qu'une seule fois pour décompter les 66 valeurs.

Et donc, en faisant comme ça, je me suis juste demandé si il était possible d'avoir un «espace d'arrivée» plus compact pour avoir moins de cellules à créer dans le tableau de décompte.

Avec «liste» ce n'est plus «direct», certes, mais en fait ça ne le sera jamais.

Avec mon questionnement de «réduction» j'interposerais une formule mathématique au lieu d'un code de 3 lignes qui est optimal. Ce serait idiot mais la question math demeure, et ça tombe, c'est peut être également trivial (utilisation des valeurs max, min, moyenne que sais-je...)

Et non, la liste des 66 valeurs ne suit pas de loi particulière. J'ai écrit «suite» mais c'est impropre. Je ne voulais pas dire «suite» dans le sens de «l'objet» mathématique.

Voila, merci d'avoir fait l'effort de me lire. J'ai l'impression de ne pas toujours être super clair en fait.

[tbc92]

Un tableau associatif, c'est nouveau (ça existe depuis une trentaine d'années seulement).

Tu peux dire

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
tab est un tableau associatif
tab(-1234) = 1
tab(1234567890123)=2

On peut avoir des nombres négatifs, des nombres énormes ... pas de problème. Ce tableau contient seulement 2 entrées , il occupe la même place qu'un autre tableau associatif avec 2 entrées qui seraient les nombres 1 et 2.

Tu peux même avoir :
tab1("corbeau")="oiseau"
tab1("cheval")="mammifère"
tab1("vache")="mammifère"

Après, oublions ces questions, et revenons à ta question (ou à ton jeu) : Comment trouver une formule mathématique (tu parles de logarithmes) pour 'rétrécir' les nombres.
Tu veux une formule pour rétrécir les nombres, mais veux-tu aussi la formule inverse pour retrouver la série initiale à partir des valeurs rétrécies ?
Je pars du principe que non, pour que le jeu reste amusant.

Guesset te demandais la liste complète.
Si tu as par exemple au milieu quelques valeurs consécutives : 105, 206, 207, ça coince un peu, il va falloir être plus vigilant sur la formule à trouver.

[Philtheform]

Je ne suis ni programmeur, ni matheux, vous l'aurez deviné. Et certainement un peu trop fatigué pour avoir les idées vraiment claires: ne perdez surtout pas trop de temps avec moi !

Le tableau associatif, je ne connais pas du tout. Je vais regardé si ça existe en C. Je comprends le principe mais, concrètement, je me demande comment fait le compilateur pour s'y retrouver ?

La liste entière avec laquelle je «réfléchissais » est:
47 55 62 79 87 94 103 107 110 115 118 122 143 151 155 158 167 171 174 179 182 186 199 203 206 211 214 218 227 230 234 242 271 279 283 286 295 299 302 307 310 314 327 331 334 339 342 346 355 358 362 370 391 395 398 403 406 410 419 422 426 434 454 458 466 482

C'est vrai que l'opération inverse pourrait être utile mais juste avec l'ordre on retrouve les «vraies» valeurs et, in fine, comme ça n'a pas vraiment d'application pratique qui me vienne a l'esprit, pas la peine de chercher outre mesure non plus.

J'ai comme le pressentiment que je vais avoir l'air bête quand la réponse va arriver...
Au moins j'aurais appris quelques nouveaux trucs.

[Flodelarab]

La réponse qui tombe pile vient de developpez.com lui-même. Suffit de cliquer ici.

"Table de hachage", c'est juste du mauvais franglais.

[Philtheform]

Intéressant. Merci.

[anapurna]

salut

je ne vois pas le probleme mathematique dans ta demande
tu veux simplement creer une liste d'entier sans trous ?
pour ce faire in ne faut pas prendre un tableau de la valeur maximal
mais augmenter dynamique la liste a chaque nouvelle entrée

une simple liste d'entier trie sur la valeur devrais te convenir

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
 
 
List = Liste d'Entier;
Debut 
  Pour ChaqueValeur Faire 
     Ajoute(List,ChaqueValeur)
  Fin Pour
  TrieListParValeur(List)
Fin 
 
 
Procedure Ajoute(List,ChaqueValeur);
Debut 
  I = Longueur(List);
  Agrandit(List)
  List[I]= ChaqueValeur
Fin

ce qui te donnera avec tes chiffres
List[0] = 47
List[1] = 55
List[2] = 62
List[3] = 79
List[4] = 87
.....
List[62] = 454
List[63] = 458
List[64] = 466
List[65] = 482

de cette maniere tu pourra faire une recherche dichotomique sur la taille de ta liste
en verrifiant les valeur associe

[Philtheform]

Attendez, Attendez... Je me demande si je n'ai pas baissé pavillon trop vite là?

En supposant que le code de «liste» soit celui que j'ai donné plus haut, c'est bien opti. en taille d'espace de décompte mais sur le traitement globale cela revient exactement à faire «* je prends la 1er valeur, je parcours la liste à analyser, je la décompte, je prends la deuxième valeur, je parcours la liste etc.»

Avec mon idée de «ratatinage cadré» en supposant que la fonction soit relativement simple a établir et pas trop complexe comme avec les log: oui, je vais fatalement gaspiller de la mémoire car je n'aurais jamais une formule math qui me donnera la stricte équivalence entre les 66 valeurs et leur ordre mais je gaspillerais moins de mémoire qu'avec la méthode brute et je ne parcourais vraiment qu'une seul fois la liste à analyser.

C'est sur l'ensemble du traitement que j'envisageais cette "optimisation".

Maintenant, je sais bien qu'en pratique c'est un peu ridicule/fumeux, et qu'au final, ça risque de ne rien optimiser du tout, mais bon, ça m'amuse.

Donc, si vous avez une bonne méthode de «ratatinage cadré» je suis toujours preneur.

[Flodelarab]

Je n'ai toujours pas compris.

Si tu as besoin de parcourir ton tableau pour avoir ton analyse, aucune méthode ne comprimera cela. Mais si le but est d'avoir un élément du tableau sans le parcourir, on t'a répondu.

Note : c'est tout le sens du calcul de complexité algorithmique des différentes méthodes.

[tbc92]

L'idée ici, c'est de trouver une formule de calcul qui diminue l'espace. En ayant toujours des entiers comme résultats.
Par exemple, si on dit f(x)= partieentiere((x-47)/2) , on passe d'une valeur max de 482 à un nouveau max de 217.
Et on vérifie que tous les nombres obtenus sont différents 2 à 2. Objectif atteint.
Le 'jeu', c'est d'essayer de réduire encore plus. Il y a évidemment moyen de faire beaucoup mieux. Avec des formules un peu tordues (utilisant les fonctions tan et atan), je pense qu'on arrive assez vite à moins de 100.

En fait, il y a même des formules qui vont permettre de réduire ces 66 nombres aux nombres 0 à 65. C'est certain, c'est mathématique (un polynôme de degré 65 va convenir). Ca enlève de l'intérêt du jeu, parce que en fait, ce qu'on cherche, c'est un compromis. Trouver une formule avec 5 ou 6 manipulations maximum (et pas 65 comme pour le polynôme parfait), et qui réduit pas mal.

C'est plus un jeu qu'autre chose. Avec les outils informatiques d'aujourd'hui, il y a des solutions de contournement 1000 fois plus efficaces que ce traitement de ratatinage.

Ici, on parle de remplacer un tableau qui occupe 1Ko en mémoire à tout casser par 20 ou 30 lignes de programme, qui vont occuper éventuellement plus d'espace mémoire que le tableau en question dans le programme final, et qui vont demander une gymnastique intellectuelle importante.

[wiwaxia]

Je crois que ton blocage vient de ce que tu raisonnes en mathématicien, en imaginant une fonction monotone croissante y = F(x) qui à toute valeur entière de (x) ferait correspondre la donnée (y) de rang (x) présente dans la liste; et qu'il suffirait ainsi de recourir à la fonction réciproque x = F^-1(y) pour trouver le rang de toute valeur (y).

S'il est relativement facile de bricoler une fonction dont le graphe passe par tous les points (x_k, y_k) de la liste, le passage à la fonction réciproque se révèle pratiquement inenvisageable: il faut en effet que la fonction F(x) soit strictement monotone (condition nécessaire d'existence de F^-1), et même dans ce cas favorable l'obtention d'une expression explicite de F^-1(y) apparaît le plus souvent hors de portée, hormis quelques fonctions particulières très simples telles que

F(x) = A*x + B , F(x) = A*xⁿ , F(x) = A^x ou F(x) = A*Ln(x) ...

qu'on ne saurait adapter à ton nuage de points.

La recherche du rang relève non pas de l'analyse, mais de l'algorithmique: des informations t'ont été abondamment fournies sur ce point.

Si tu t'intéresse absolument à la fonction F(x), tu peux par exemple recourir au sinus cardinal normalisé

Sc(u) = Sin(π*u)/(π*u) ;

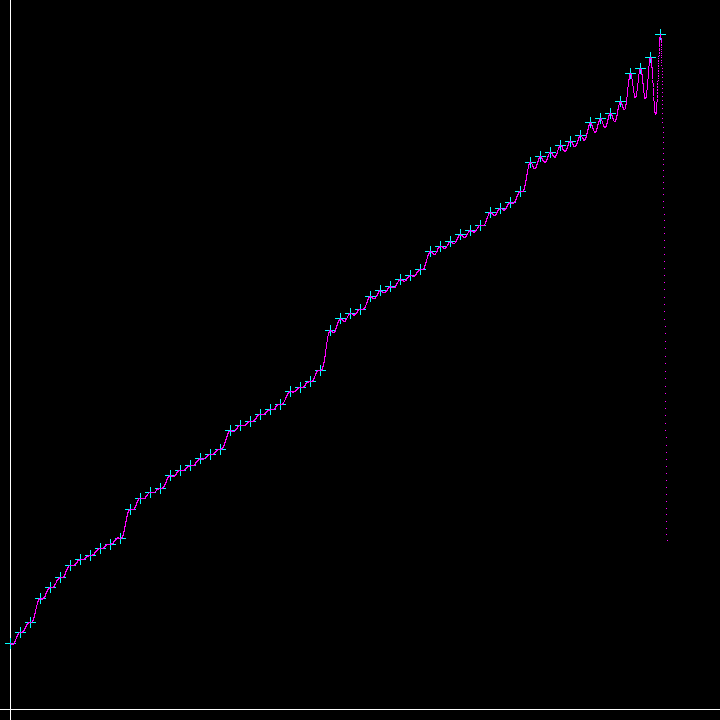
on vérifie ainsi aisément que le graphe de la fonction

F(x) = Σ_k=0^k=65(y_k*Sc²(x - x_k))

passe par les 66 points du tableau.

Le recours au carré permet d'atténuer les oscillations; elle pourraient disparaître par l'extension appropriée de la liste en ses deux extrémités.

[Philtheform]

Oui, c'est bien cela. Tbc92 a bien compris/reformulé je que je voudrais.

Et donc, il ne semble pas avoir de formule simple. En fait, il faudrait qu'elle soit sacrément simple pour qu'il y est un «gain» global sur le traitement. Ce qu'on gagnerait en mémoire, on le perdrait en vitesse d'exécution avec une formule complexe.

Mais d'un autre coté,dans l'exemple, les valeurs sont petites, si la plus grande valeur était 482 000 000, cela commencerait a faire un bien grand tableau pour décompter 66 valeurs.

En plus, mon avis que:

(0)

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
for(i=0;i<size_Data;++)
	Tab_decpte[Data[i]]++

C'est «mieux» que:

(1)

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
Val[66][2]={(47,0),...(482,0)}
For(i=0;i<66;i++){
	For(j=0;j<size_Data;j++){
		if(Data[j]=Val[i][0]
			Val[i][1]++
	}
}

Je n'en suis même pas certain. C'est mieux pour une feignasse comme moi en nombre de lignes à écrire mais après...

Les réponses avec les «liste» «table associative» mon un peu dérouté mais comme en fait la version minimale pour «contracter» serait selon moi:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
Liste(x){
	Val[66]={42,...,482}
	for(i=0;i<size_val,i++){
		if(x=Val[i]
			return i
}
 
for(i=0;i<size_Data;++)
	Tab_decpte[Liste(Data[i])]++

et que cela reviens a faire (1) autrement. Toute les réponses avec les structures de données ne vont pas car, en caricaturant au max, cela revient a «Liste» en plus compliqué. A un moment donné dans le code du traitement de la structure, il y aura toujours le parcours d'un tableau et cela revient à faire (1)

J'ai regardé le code de «Table de hachage» qu'a donné Flodelarab. Au début ça fait peur mais ce n'est pas si «compliqué» que ça (Enfin, c'est facile à dire avec la solution, hein) et il y a bien un parcours d'adresse mémoire pour faire le lien. D'ailleurs, je ne vois pas comment il pourrait en être autrement. Si vous avez un technique qui donne la valeur d'une clé sans parcourir la table, n'hésitez pas à me l'expliquer.

Attention, il n'est pas exclu que je fasse de fausse équivalence car je ne doute pas qu'il existe des façons sophistiquées de «parcourir» les tables. Mais, ça va trop loin là.

Donc, pour en revenir a ma tentative «d'amélioration» de (0), je me suis dis que créer 482 cellules, c'est beaucoup quand même (je sais, c'est ridicule...) et de me demander si je ne pourrais pas faire pareil mais en créant moins de cellules.

Avec un vague souvenir de graphique en échelle logarithmique qui «comprime» les fortes valeurs, j'ai bidouillé en 2 minutes les formules que j'ai mise au début.

(0) «amélioré» serait:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
Ratatinage(x){
	y=tronque[x-[(3,8*x)/Ln(x)]]
        return y
}
 
for(i=0;i<size_Data;++)
	Tab_decpte[Ratatinage(Data[i])]++

La valeur décomptée ne coïncide plus avec l'adresse dans Tab_decpte comme dans le cas (0), par exemple 482 arrive désormais à l'adresse 185 dans Tab_decpte mais ce n'est pas grave car c'est toujours la 66ieme valeur non nulle dans Tab_decpte, je peux toujours retrouvé la valeur décomptée et j'ai gagné 227 cellules.

Je pense désormais que c'était bien naïf d'espérer trouver une fonction simple qui ferait mieux que (0) ou même (1)

Déjà, le 3,8 dans la formule, je l'ai trouvé par tâtonnement. Si je ne sais pas le calculer c'est mort. Bien évidemment, les 66 valeurs je ne les connais pas d'avance.

J'espère que c'est plus intelligible expliqué ainsi.

[tbc92]

Les échelles 'logarithmiques', tu en parles à différentes reprises, c'est bien, mais pas adapté ici.
Si tu regardes comment tes données sont réparties (le dessin de wiwaxia est très explicite), tes 66 points sont globalement alignés.
L'écart entre la 1ère valeur et la 11ème, ou l'écart entre la 51ème et la 61ème, c'est en gros le même.

Donc oublie les logarithmes.
Les log, c'est adapté quand on a le même pourcentage d'évolution entre les valeurs : en gros si on double toutes les 10 valeurs , alors c'est adapté. Ici, entre la 1ère et la 6ème, on double (94 est le double de 47) ; est-ce qu'on double toutes les 5 valeurs ? non... loin de là, la tendance sur les première valeurs ne se poursuit pas du tout.

[anapurna]

Salut

pourquoi parcours-tu ta liste avec une boucle for

alors que si ta liste est trié une recherche dichotomique
te permet de diviser le temps de recherche

Exemple

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
 
Fonction recherche_dichotomique(tab, val)
FAIRE
   gauche = 0
   droite = len(tab) - 1
   Tanque gauche <= droite Faire 
   FAIRE                                              
      milieu = (gauche + droite) / 2  # on a besoin que du quotient
      SI tab[milieu] = val ALORS       # on a trouvé val dans le tableau,
         retourne milieu   # à la position milieu
      SINON 
         SI  tab[milieu] > val ALORS  # on cherche entre gauche et milieu - 1
           droite = milieu - 1
         SINON                             # on a tab[milieu] < val
             gauche = milieu + 1    # on cherche entre milieu + 1 et droite
        FINSI
     FINSI
   FINFAIRE
   retourne -1 # on est sorti de la boucle sans trouver val
FINFAIRE

[kaitlyn]

Salut,

Je pense désormais que c'était bien naïf d'espérer trouver une fonction simple qui ferait mieux que (0) ou même (1)

Déjà, le 3,8 dans la formule, je l'ai trouvé par tâtonnement. Si je ne sais pas le calculer c'est mort. Bien évidemment, les 66 valeurs je ne les connais pas d'avance.

Dans ce genre d'exercice, le but n'est pas de trouver une solution, mais une solution générique.
Si on ne peut ni la réutiliser ni la réadapter, elle n’est pas rentable.

L'approche qui ressemble le plus à ce que tu veux faire est effectivement le tableau associatif, plus connu sous le nom de dictionnaire. Tu passes ta clé à une fonction, elle calcule un index qui te renvoie directement à sa valeur.