Bonjour,
Parmis toutes les objets mathématiques qu'il est souvent necessaire de calculer sur les pixels d'une image, il y en a deux qui reviennent assez souvent:
- Le vecteur Gradient, c'est a dire les derivées partielles du 1er ordre de l'intensité:
- La matrice Hessienne, c'est a dire les derivées partielles du 2nd ordre de l'intensité:
Code : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4dI(x,y) dI(x,y) G(x,y) = ( ------- , -------- ) dx dy
Remarque: la trace de cette matrice est appelé "Laplacien"
Code : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
8| d²I(x,y) d²I(x,y) | | -------- -------- | | dx² dxdy | H(x,y) = | | | d²I(x,y) d²I(x,y) | | -------- -------- | | dxdy dy² |
De part la nature discrete d'une image numérisée, les derivées sont approximées par des différences d'intensité au voisinage du pixel. Ces calculs vont dont etre tres sensibles au bruit. Pour limiter les effets du bruit, il est d'usage de lisser préalablement l'image (en la convoluant par une Gaussienne) avant de calculer les derivées.
Et c'est la que la magie de la convolution intervient car:
Donc on peut inverser le calcul: d'abord calculer les derivées de la Gaussienne, puis convoluer ce résultat avec l'image. Cela nous donne deux avantages:
Code : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4d dF(t) ---- [ F(t) * I(t) ] = [ ----- ] * I(t) dt dt
- Réduire les calculs de derivées partielles de l'intensité à des convolutions.
- Précalculer les noyaux de convolution, car ils sont indépendants de l'image.
Calculons les dérivées partielles de la Gaussienne:
Derivées partielles du 1er ordre
Code : Sélectionner tout - Visualiser dans une fenêtre à part
2
Code : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
8
Derivées partielles du 2nd ordre
Quelques remarques sur les noyaux de convolutions obtenus:
Code : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
8
9
10
11
12
13
14
1. Modifiez la valeur centrale du noyau afin que la somme des coefficients de la matrice soit égale a zero. Cela permet de s'assurer que la dérivée partielle sera nulle sur une zone d'intensité uniforme.
2. Choisissez une taille minimum de 3x3 pour le Gradient et 5x5 pour la Hessienne. En effet, plus la dérivée est d'un ordre élevé, plus il faut de points pour la calculer.
3. La valeur de sigma² permet de moduler la force du lissage (generalement une valeur entre 1 et 3 pour le Gradient, et entre 2 et 5 pour la Hessienne)
Exemple de code en Java:
Code Java : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
Code Java : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51













 Répondre avec citation
Répondre avec citation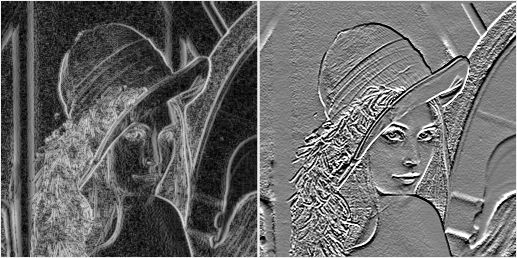






 Quel rapport avec le calcul du Gradient/Hessienne ?
Quel rapport avec le calcul du Gradient/Hessienne ?
Partager