Inscrivez-vous gratuitement
pour pouvoir participer, suivre les réponses en temps réel, voter pour les messages, poser vos propres questions et recevoir la newsletter
Tu as raison, si on relit les puits aux sources n'importe comment quand le graphe est faiblement connexe. Cela ne marche pas.Envoyé par dividee
Donc s'il n'y a pas de règles spéciales pour le cas là, ton programme ne marchera pas.
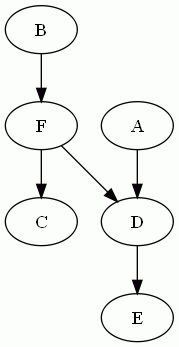
Par exemple pour le graphe,
Tu peux relier C à B et E à A, mais ce n'est pas bon (pourtant, on a bien relié toutes les sources et les puits entre eux)
@bredelet : Tu peux donner le principe général de ton algo ?
Notamment avec des mots comme : On détermine les composantes fortements connexes, on calcule les puits et les sources etc.
Il faut lier les puits a des sources qui ne les dominent pas. Mais j'ai pas le temps de reflechir a cela.
Je commence avec l'idée de Jedai de réduire les composantes fortement connexes à un noeud.
Étant donné un graphe sans composante fortement connexe. Je vais définir une "composante en étoile" comme une source et tous les chemins qui en sortent.
Par exemple dans le graphe de millie, les "composantes en étoile" sont BFCDE et ADE.
Je m'assure que chaque composante en étoile est reliée à une autre en ajoutant les arêtes puits -> source nécessaires. Cela génère le graphe en étoile.
Si je reprends le même exemple de graphe, je pourrais choisir B comme première source. Il y a deux puits, C et E. Ajouter une arête C -> A pour relier les composantes ensemble.
Pour la solution minimale il faudrait détecter que E appartient aussi à la composante ADE pour éviter un cycle inutile (choix E -> A). Quand il n'y a plus de choix alors on peut ajouter une arête qui crée un cycle jusqu'à obtenir le graphe en étoile. Ceci manque dans mon algo.
À ce point là pour obtenir un graphe fortement connexe il suffit de relier chaque puits restant à l'unique source par une arête.
En y réfléchissant, le simple fait que D ait plus d'une arête entrante indique que le choix de E n'est pas le meilleur. Cela montre que DE appartient aussi à une autre composante. À un point donné on va forcément ajouter un arête vers la source de cette autre composante, créant un cycle.
Il faudrait donc distinguer les "puits appartenant à une seule composante" des "puits appartenant à plusieurs composantes". Il faut se servir des puits dans le premier groupe en priorité.
Bonjour,
Voici ma proposition:
1) réduire le graphe initial en composants fortement connexe. On travaille ensuite avec le nouveau graphe.
Dans le graphe d'exemple on pourrait regrouper les noeuds (A,C,D). Le nouveau graphe serait {B, (ACD), F}.
2) On va chercher à compléter pour chacun des noeuds un arc entrant et un arc sortant s'ils n'en possèdent pas déjà. Pour cela on va modéliser un problème de maximisation de flot à résoudre par l'algo Ford-Fulkerson: le graphe de FF sera constitué successivement de:
- une "source"
- un ensemble (S) de noeuds constitués de noeuds du graphe réduit ayant besoin d'un arc sortant
- un ensemble (E) de noeuds constitués de noeuds du graphe réduit ayant besoin d'un arc entrant
- un "puits"
Dans notre exemple (S) = {B,F} et (E)={(ACD),F}
on relie la "source" à l'ensemble (S) , on relie tous les noeuds (S) à (E) et on relie (E) à "puits" sauf les noeuds qui représente le même noeud du graphe initial. Chaque arc a un poids de 1.
Une fois qu'on a fait tourner l'algo FF sur ce graphe, chaque flot qui passe d'un noeud de (S) vers un noeud de (E) se traduit par un arc dans le graphe initial reliant les noeuds en question.
3) A la fin de l'ago FF tous les noeuds de (S) n'ont pas forcément un flot sortant ni les noeuds de (E) un flot entrant. On recommence l'algo à partir de l'étape 1 (modifié).
@cleth :
Je suis pas sûr que ta méthode marche
Sur le graphe :
Tu peux te retrouver à prendre une source A et le puit E, et tu ne pourras passer les flots que de A à E (ce qui n'est pas un arc optimal).
Note: J'ai modifié la dernière étape de mon algo. Tant qu'on n'a pas tout réduit on recommence.@cleth :
Je suis pas sûr que ta méthode marche
Sur le graphe :
Tu peux te retrouver à prendre une source A et le puit E, et tu ne pourras passer les flots que de A à E (ce qui n'est pas un arc optimal).
Ma méthode marche car dans ton exemple l'ensemble (S)={C,E} et (E)={A,B}
donc l'algo FF donnera soit (C,A) et (E,B) soit (C,B) et (E,A).
Dans le premier cas on a la solution. Dans le deuxième cas on se retrouve à boucler encore une fois l'algo et ajouter un arc supplémentaire.
Donc cet algo n'est pas optimal
(Mais je vais n'abandonne pas)
Oui, quand je dis marche, ça veut dire optimal ^^ (puisque c'est le but du défi).N
Donc cet algo n'est pas optimal
Courage(Mais je vais n'abandonne pas
Après réflexion (et déjeuner
1) réduire le graphe initial en composants fortement connexe. On travaille ensuite avec le nouveau graphe.
Dans le graphe d'exemple on pourrait regrouper les noeuds (A,C,D). Le nouveau graphe serait {B, (ACD), F}.
2) On va chercher à compléter pour chacun des noeuds un arc entrant et un arc sortant s'ils n'en possèdent pas déjà. Pour cela on va modéliser un problème de maximisation de flot à résoudre par l'algo Ford-Fulkerson: le graphe de FF sera constitué successivement de:
- une "source"
- un ensemble (S) de noeuds constitués de noeuds du graphe réduit ayant besoin d'un arc sortant
- un ensemble (E) de noeuds constitués de noeuds du graphe réduit ayant besoin d'un arc entrant
- un "puits"
on relie la "source" à l'ensemble (S) , on relie tous les noeuds (S) à (E) et on relie (E) à "puits" sauf les noeuds qui représente le même noeud du graphe initial. Chaque arc a une capacité de 1 et un coût défini comme suit: soit un arc de X(S) vers Y(E) le coût est zéro si dans le graphe initial il n'existe pas de chemin de Y vers X et un dans le cas contraire.
Une fois qu'on a fait tourner l'algo FF sur ce graphe pour trouver le flot maximal et à coût minimal, chaque flot qui passe d'un noeud de (S) vers un noeud de (E) se traduit par un arc dans le graphe initial reliant les noeuds en question.
3) Si à la fin de l'ago FF le graphe n'est pas fortement connexe On recommence l'algo à partir de l'étape 1.
Je ne suis pas toujours convaincu que ça marche.
Tu peux dérouler ton algo sur mon exemple ?
Si tu choisis mal ton puit et ta source, le calcul de flot maximal ne pourra amener à rien sur mon exemple puisque tu ne peux pas forcement rejoindre le bon puit à partir de la source.
Sur cet exemple mon algo va donner:@cleth :
Ensemble (S)={C,E} (je devrais mettre un indice s sur C et E pour être plus clair)
Ensemble (E)={A,B}
Le graphe complet pour l'algo FF est constitué des arcs suivants:
(source, C) capacité 1, coût 0
(source, E) capacité 1, coût 0
(C,A) capacité 1, coût 0
(C,B) capacité 1, coût 1
(E,A) capacité 1, coût 1
(E,B) capacité 1, coût 0
(A, puits) capacité 1, coût 0
(B, puits) capacité 1, coût 0
Le résultat de cet algo FF des flots sur les arcs:
(source, C)
(source, E)
(C,A)
(E,B)
(A, puits)
(B, puits)
Le flot total est 2 avec un coût total de 0
Donc le résultat de cette étape c'est l'ajout de 2 arcs (C,A) et (E,B)
Et l'algo s'arrête là car le résultat est un graphe fortement connexe.
ps: j'appelle "source" et "puits" deux noeuds qui servent juste pour l'algo FF et qui sont indépendants du graphe initial.
Je ne comprend pas ce que tu appelles un coût ?
A quoi sert-il ?
Je vois bien ce qu'est une coupe, mais ce n'est pas un entier mais un ensemble de couple de sommets. Une coupe peut avoir une capacité (qui est d'ailleurs minimal quand le flot est maximal) et un flot relatif à un flot.
source et puit sont donc 2 autres sommets ?
Un coût c'est juste un critère à optimiser. Je ne vois pas pourquoi tu parles de "coupe" ?
Sinon dans un problème de "flot maximum" on ajoute en général 2 noeuds particuliers source et puits sauf si ça existe déjà dans le problème initial.
Pour visualiser, on peut considérer la "source" comme un robinet d'eau. Les arcs qui relie tous les sommets depuis la source sont des tuyaux. La capacité d'un arc est la section du tuyau. Le puits c'est le noeud final où toute l'eau se vide quand on ouvre le robinet.
Dans l'algo FF si on a un arc (A,B) de capacité 3 de coût 2, on peut au cours de l'algo décider de faire passer un flot de 2 unités (<3) et le coût est 2x2.
Le flot total est la somme des flots qui partent de la source qui est égale à la somme des flots qui arrivent au puits. Le coût total à minimiser est la somme de chaque flot sur un arc multiplié par le cout unitaire de l'arc.
Pour notre problème les capacités sont égales à 1 et les coût sont soit 0 soit 1. Les unités de flots qui passent par un arc est de soit zéro soit 1 (pas de fraction).
Je comprenais pas pourquoi tu faisais :
Là, on aurait dît que tu reliais la source aux sommets qui sont des puits.(source, C) capacité 1, coût 0
(source, E) capacité 1, coût 0
Et pour le coût, c'est juste que je n'ai jamais entendu parlé de coût dans les problèmes de flot maximal
Tu entends quoi par : le résultat ?Le résultat de cet algo FF des flots sur les arcs:
(source, C)
(source, E)
(C,A)
(E,B)
(A, puits)
(B, puits)
FF retourne juste le flot maximal, il peut y avoir plusieurs configurations possibles.
Je peux dérouler cet algo sur d'autres exemples si tu veux.
Je suis en train de chercher une démo pour cet algo.
Tout ce que je peux dire pour l'instant c'est que la fonction coût permet de privilégier les cycles les plus longs.
Dans ce cas il n'y a qu'une seule configuration possible qui minimise le coût.
Le résultat c'est le flot qui passe par ces arcs. la somme total du flot est 2.
Le coût total est 0.
Si on considère cette configuration de flot:
(source, C)
(source, E)
(C,B)
(E,A)
(A, puits)
(B, puits)
Le coût serait de 2 (le flot étant toujours égal à 2) donc pas minimal.
L'ajout de la fonction coût écarte cette configuration.
Pour être exact, l'algo que j'ai connu est du "FF modifié".
Un coup de google m'apprend que le nom exact est l'ago de Busacker et Gowen.
En fait, dès que le graphe est faiblement connexe, il y a une méthode vachement plus simple que de passer par des flots.
Donc, peut être que ta méthode est bonne (il y a peut être des contre exemples, mais je n'ai pas tout compris), mais elle doit être assez hard à prouver.
Vous avez un bloqueur de publicités installé.
Le Club Developpez.com n'affiche que des publicités IT, discrètes et non intrusives.
Afin que nous puissions continuer à vous fournir gratuitement du contenu de qualité, merci de nous soutenir en désactivant votre bloqueur de publicités sur Developpez.com.
Répondre avec citation
Partager