Salut!
Si j ai deux vecteurs A(N) et B(N) qu elle est la definition exacte de A*B?
merci
Salut!
Si j ai deux vecteurs A(N) et B(N) qu elle est la definition exacte de A*B?
merci
comme le dit wikipedia:
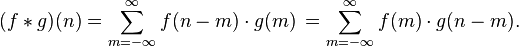
ALGORITHME (n.m.): Méthode complexe de résolution d'un problème simple.
oui, mais mes tableaux sont de dimensions finie:
A(N), et B(N) (pas infinie)
ALGORITHME (n.m.): Méthode complexe de résolution d'un problème simple.
pas totalement convaincu, car sur scilab par exemple , je lui exrit le code suivant il le omprend :
Code : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
8
les fonctions ont été étendues avec des zéros, et l'ensemble de définition du produit de convolution a été réduit a 7 valeurs (len(x)+len(z)-1). Les 7 valeurs pour lesquelles les produit de convolution utilise des valeurs connues de x et z
ALGORITHME (n.m.): Méthode complexe de résolution d'un problème simple.
mais ensuite comment utilser alors les FFT pour calculer sous forme FFT^^(-1)(FFT(g)FFT(f))
ALGORITHME (n.m.): Méthode complexe de résolution d'un problème simple.
en fait, Tu as la relation suivante :
(A*B)=FFT^(-1)(FFT(A)*FFT(B)), avec FFT etant la transformee de Fourier rapide . et la transformee de Fourier rapide agit sur les tableaux de dimension finie. On utilise cette relation pour acceler le code.
le but c est de calculer A*B avec cette relation
Ah, Tu veux dire remplacer le produit de convolution par un produit complexe dans le domaine fréquentiel. Oui effectivement c'est plus rapide si tes fonctions/vecteurs ont beaucoup de valeurs (plus de 60).
ALGORITHME (n.m.): Méthode complexe de résolution d'un problème simple.
oui, mais le probleme, c est que j ai une double B(j1,j2)=double somme de A(j1-l1,j2-l2)*phi(j1,j2), si je suppose que l1 et l2=1,M , alors j1 et j2 varie d ou jusau ou?
Déjà, si tu calcules B(j1,j2), ta double somme doit plutôt être:
B(j1,j2)=Σ Σ A(j1-l1,j2-l2)*phi(l1,l2)
Dans la théorie l1,j1,l2 et j2 varient de - l'infini à + l'infini.
Mais comme on va étendre les fonctions A et phi avec des "0", ca ne sert a rien d'aller aussi loin car multiplier des valeurs par "0" ne changera pas la somme. Donc on se limite a l'ensemble de définition de A et phi.
si A est un tableau de taille MxM et phi un tableau de taille L*L, ca doit faire un tableau de taille (M+L-1)*(M+L-1) pour B
ALGORITHME (n.m.): Méthode complexe de résolution d'un problème simple.
bon si je suppose que B(j1,j2)=Σ Σ A(j1-l1,j2-l2)*phi(l1,l2), j1,j2=-M1,M1-1 de meme l1 et l2. comment utiliser les FFT dans ce cas? les souroutine de FFT commence de 1
merci
Tu calcules FA=FFT(A) et Fphi=FFT(phi). Cela te donne 2 vecteurs de valeurs complexes.
Tu multiplies deux a deux chaque composante des vecteurs (attention, c'est une multiplication de nombres complexes)
FAFphi = { FA[1]*Fphi[1], FA[2]*Fphi[2], ... , Fphi[M]*FB[M] }
Et tu prends la transformée inverse B = FFT^-1( FAFphi )
ALGORITHME (n.m.): Méthode complexe de résolution d'un problème simple.
par contre mon A et B sont des matrices, pas des vecteurs
ALGORITHME (n.m.): Méthode complexe de résolution d'un problème simple.
Le calcul d'une convolution discrète par une transformation de Fourier discrète donne pour résultat la convolution circulaire des deux suites, pas la convolution linéaire.
Pour obtenir la convolution linéaire, il faut étendre les suites, par des zéros, à (au moins) la dimension finale de la convolution linéaire (L+M+1) et faire les transformées de Fourier discrètes sur cette dimension.
Partager